Page 141 - ele_math_6-1_teacher

수업 일자 숙제

문 제 문제 해결 | 추론 | 의사소통
해결 두부의 부피와 겉넓이 구하기 2 민수는 자르기 전 두부와 자른 두부 2조각의 겉넓이를 비교하려고 합니다. 물음에 답하세요. 6
결
해
● ● 자르기 전 두부의 겉넓이를 구해 보세요. (10\10)\2+(10+10+10+10)\5
=400 (cm^2)
● ● 자른 두부 2조각의 겉넓이를 민수의 방법으로 구해 보세요.
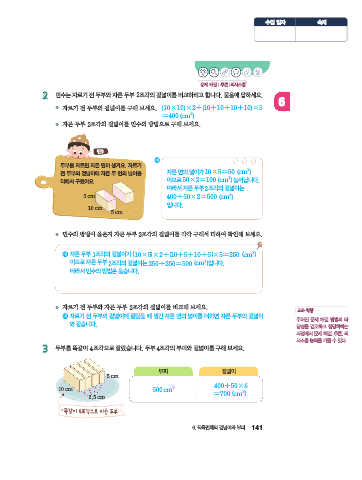
직육면체 모양의 두부를 똑같이 2조각으로 잘랐습니다.
두부의 부피와 겉넓이를 알아보세요.
민수

두부를 자르면 자른 면이 생겨요. 자르기
전 두부의 겉넓이에 자른 두 면의 넓이를 자른 면의 넓이가 10\5=50 (cm^2)
더해서 구했어요. 이므로 50×2=100 (cm^2) 늘어납니다.
따라서 자른 두부 2조각의 겉넓이는
5`cm 5`cm 400+50\2=500 (cm^2)
입니다.
10`cm
10`cm 5`cm
5`cm
5`cm
10`cm 똑같이 2조각으로 자른 두부 ● ● 민수의 방법이 옳은지 자른 두부 2조각의 겉넓이를 각각 구해서 더하여 확인해 보세요.
10`cm
자르기 전 두부  자른 두부 1조각의 겉넓이가 (10×5)×2+(10+5+10+5)\5=250 (cm^2)

이므로 자른 두부 2조각의 겉넓이는 250+250=500 (cm^2)입니다.
따라서 민수의 방법은 옳습니다.

1 자르기 전 두부와 자른 두부 2조각의 부피를 비교해 보세요.

● ● 부피를 구해 보세요.
● ● 자르기 전 두부와 자른 두부 2조각의 겉넓이를 비교해 보세요.
교과 역량
자르기 전 두부 자른 두부 2조각  자르기 전 두부의 겉넓이에 잘랐을 때 생긴 자른 면의 넓이를 더하면 자른 두부의 겉넓이
주어진 문제 해결 방법의 타
와 같습니다. 당성을 검토하고 정당화하는
과정에서 문제 해결, 추론, 의
3
3
10×10×5=500 (cm ) 10×5×5+10×5×5=500 (cm ) 사소통 능력을 기를 수 있다.
3 두부를 똑같이 4조각으로 잘랐습니다. 두부 4조각의 부피와 겉넓이를 구해 보세요.

부피 겉넓이
● ● 자르기 전 두부와 자른 두부 2조각의 부피를 비교해 보세요. 5`cm
 두부를 잘라도 부피는 변하지 않습니다. 10`cm 500 cm^3 400+50×6
=700 (cm^2)
2.5`cm
● ● 두부를 똑같이 8조각으로 자른다면 자른 두부의 부피는 어떻게 될지 이야기해 보세요.
똑같이 4조각으로 자른 두부
 두부를 8조각으로 잘라도 부피는 변하지 않을 것 같습니다.
140 수학 6 - 1 6. 직육면체의 겉넓이와 부피 141

20개정_초등_수학[616](123~146)_수정본OK.indd 140-141 2022. 4. 27. 오후 2:36

20개정_초등_교사용_수학[616](123~146)_사교.indd 141 2022. 7. 4. 오후 4:58