Page 315 - ele_math_6-2_tutor

9 단원의 1. 원기둥, 원뿔, 구의 개념
이론적 배경
가. 원기둥
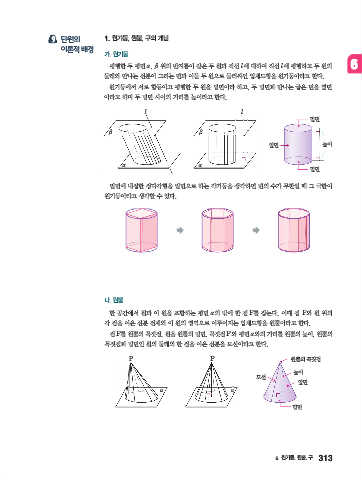
평행한 두 평면 alph, beta 위의 반지름이 같은 두 원과 직선 l에 대하여 직선 l에 평행하고 두 원의 6
둘레와 만나는 선분이 그리는 면과 이들 두 원으로 둘러싸인 입체도형을 원기둥이라고 한다.
원기둥에서 서로 합동이고 평행한 두 원을 밑면이라 하고, 두 밑면과 만나는 굽은 면을 옆면
이라고 하며 두 밑면 사이의 거리를 높이라고 한다.

l l l l l l
߃ݶ
߃ݶ ߃ݶ
β β β β β β
֫੉
৖ݶ
৖ݶ ৖ݶ ֫੉ ֫੉
α α α α α α
߃ݶ
߃ݶ ߃ݶ
밑면에 내접한 정다각형을 밑면으로 하는 각기둥을 생각하면 변의 수가 무한일 때 그 극한이
원기둥이라고 생각할 수 있다.

나. 원뿔
한 공간에서 원과 이 원을 포함하는 평면 alph의 밖에 한 점 P를 잡는다. 이때 점 P와 원 위의
각 점을 이은 선분 전체와 이 원의 영역으로 이루어지는 입체도형을 원뿔이라고 한다.
점 P를 원뿔의 꼭짓점, 원을 원뿔의 밑면, 꼭짓점 P와 평면 alph와의 거리를 원뿔의 높이, 원뿔의
꼭짓점과 밑면인 원의 둘레의 한 점을 이은 선분을 모선이라고 한다.

ਗࡻ੄ ԙ૙੼
P
PP PP ਗࡻ੄ ԙ૙੼ਗࡻ੄ ԙ૙੼
P
֫੉֫੉
֫੉
ݽࢶݽࢶ
ݽࢶ
৖ݶ
৖ݶ৖ݶ
α
α
αα αα
߃ݶ
߃ݶ߃ݶ

6. 원기둥, 원뿔, 구 313

20개정_초등_지도서[626](305~340)_수정본OK.indd 313 2022. 4. 28. 오후 12:42